sad but true, lines are not surfaces. time to remedy this :)

if we close a polyline – its starting point is the same as its ending point – then it becomes a polygon. unlike a polyline, a polygon describes a surface. the smallest possible surface is a triangle and all surfaces can be boiled down to a series triangles. this process is called tesselation or triangulation.
a triangle has numerous properties and so many applications in computational geometry that Frank has done a full length exposé at the FFK, the FOTB and more recently at the AUGXL. I had a chance to attend the latter two and have to say that the FOTB’s session was epic.

two words about Alan shaw: “he rocks”.

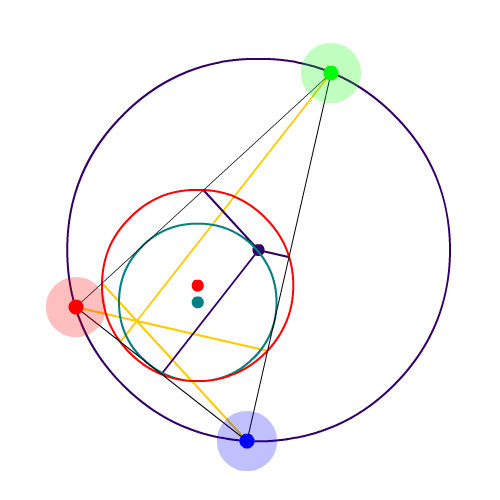
if a triangle bears the individual properties of the points, the lines, the segments and the polylines, they also have a lot of interesting properties and here are some of them.

drag the handles to view better what each thing does.
you can open it in a new window to see it fullscreen.
warning: I don’t have a scientific background and have a very shallow level of abstraction. please forgive me if something I say is not right and feel free to correct me.

• medians & gravity center (aka centroid) the medians join each vertex to the center of the opposite side. their intersection is the centroid, it’s always contained inside the triangle.
• altitudes & orthocenter the altitudes go through each vertex and are perpendicular to the opposite side. their intersection is called the orthocenter. it can be set outside of the triangle.
• bisectors, incircle & excircles the bisectors split each angle into 2 equal angles. their intersection is the incircle’s center. the incircle is the smallest circle fitting inside the triangle. the radius of the incircle is found by projecting the center onto each side of the triangle and choosing the shortest distance. the excircles are very well described here ( < laziness )
• perpendicular bisector & circumcircle those are closely related to the delaunay triangulation : the circumcircle is used to tell wether a point is valid in the delaunay set. the perpendicular bisectors are used to draw the voronoi diagram. also the circumcircle’s center is equidistant to the 3 points of the triangle. useful tools :)
• the euler line & euler circle the line goes from the orthocenter to the circumcircle’s center through the centroid. the [ centroid-orthocenter ] length is 2 thrid of the euler line’s length. the euler circle goes through all three altitudes’ intersections with the triangle’s sides and through all three perpendicular bisector’s intersections with the triangle sides. to be honest, I don’t know what they’re used for…
• it has an area.
• it has an inside and an outside
• it has a front and a back aka culling (the triangle should be drawn in pale grey if turned backwards )

there are two special cases where the triangle won’t help very much:
- 2 or 3 points of the triangle have the same coordinates.
- all 3 points lie on the same line
in the demo, it would look like:

“Mondrian here I come!” ^^
mistakes and accidents are very interesting, sometimes even more interesting than the result we want to achieve.

apart from these special cases:
- a triangle is always simple (not self-intersecting), this is importnat for computations.
- all its points (vertices) lie on the same plane, in 2D and in 3D.

so the simplest surface is very complex and using it much more difficult than simply drawing lines but – rejoyce – the results are far more interesting too.

- by combining triangles, we obtain a mesh that allows countless applications ( morphing, distorsions [long list here] )
- 2D physics: as it is the smallest possible surface and as it is always convex, we can build a physics system on top of it ( calculate masses, areas, moment of inertia, perform in/out tests etc. )
- 3D. as it is the simplest surface also in 3D, it is used to build, subdivide and render meshes.

btw the molehill thing is all about triangles or more precisely “delegating the triangle rendering process to the GPU” :)

before addressing the MESH, we’ll have a look at REGULAR POLYGONS. they have some interesting properties and are far less difficult to use. but before that, some classes could prove useful.
so, next step: USEFUL TOOLS ! for the masses

Tags: basics, generative, generative art, geometry, introduction, properties, triangle