as seen in the last article, one dimension is the relationship between two values or two states of an object.
this relationship can be quantified which allows us to normalize and interpolate a value between 2 values.
as we’re interested in graphics, it enabled us to draw a line between 2 points.

now what if we add a second line?

then we have two lines ! mwhahaha !
…ok, sorry.

actually, creating a line was a shortcut for us to understand the concept of dimension and try to explore its richness. Unfortunately with what we’ve seen so far, we couldn’t draw a 2D line for we’d need a 2nd dimension to draw it onto. by the way, a signle dimension can barely be thought of as such: it’s like thinking of the time passing ; unless it leaves traces on an object, there’s no way to “experience” or “represent” the time itself.

that line we drew was a 2D line already, let’s explore the 2D space.

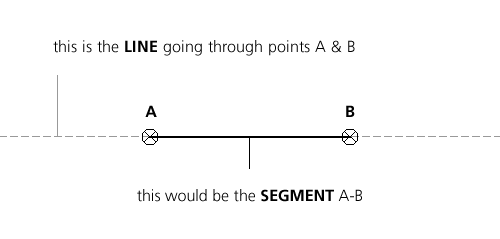
a line is infinite and goes through 2 points.

if 2 lines are coincident (line goes through the same points), we’ll remain in one dimension. and no matter how many coincident lines we’ll add, they’ll remain in their single dimension… sad.
now if they are not coincident, there’s another special case that we’re going to see first : they can be parallel. 2 parallel lines are supposed never to cross each other except maybe at an infinite length but who cares…

give the animtion the focus then left / right to navigate.

• 0 – 2 parallel lines
• 1 – OMFG we have a regular 2D space !
• 2 – let’s put lots of them !
• 3 – and randomize their start / end ratios to get different lengths
• 4 – and give them random thicknesses and .. move them !
• 5 – and … and put some glow ! … and move them in the other direction! woohoo !
• 6 – as it is a 2D space, we can cross the lines and obtain a grid. grids are extremely useful in design and generative art, they allow us to split the space into smaller spaces.
• 7 – variations on the grid: the column / row count is set at random, the thickness of the lines is based on an ondulating function. we the stroke are thick enough, it provokes an optical illusion called the “Herman grid illusion“. love it :)
• 8 – is when we randomize distribution, start/end points, thickness and alpha. Piet Mondrian spent his life doing this and don’t go thinking he’s a moron ; this composition issue and the ability to solve it is what makes the difference between an artist and a wannabe.
• 9 – moving the grid start/end points will keep lines parallel and produce an interesting pattern. like a rotozoom
• 10 – it can also be rendered in different ways

parallel are interesting because they create order, a bit like the grid or the frame points distribution.
the bauhaus, then the concrete art and later the op (or kinetic) art played with regular sets of lines and shapes to create movement or to structurate space. by overlaying sets of grids, one can easily create extremely complex patterns.
this is a great part of François Morellet‘s work (quoted in the AUGXL diaporama). he uses regular grids, overlays them in 2D or 3D.
for instance and directly inspired (=stolen) from Morellet’s work, this snippet :

private function gridComposition():void 
{
	var bd:BitmapData = new BitmapData( 16, 16, true, 0 );
	bd.fillRect( new Rectangle( 0, 0, 1, bd.height ), 0xFFFFFFFF );//draws a white vertical stripe 
	var matrix:Matrix = new Matrix();//used for the rotations
	
	var total:int = 8; //grids count
	var angle:Number = ( Math.PI / total ); // 180 ° not to leave too many trails ! 
	for ( var i:int = 0; i < total; i++ )
	{
		matrix.rotate( angle );
		graphics.beginBitmapFill( bd, matrix, true, true );
		graphics.drawRect( 0, 0, stage.stageWidth, stage.stageHeight ) ; 
	}
}

gives if total = 3

total = 8

so with very little means, we can achieve great results.
this should never be forgotten :)

truth be told, even though parallels are very rich, they are boring.
fortunately for us, lines have some interesting properties in 2D space.

for instance a slope:

static public function slope( p0:Point, p1:Point ):Number{	
	return ( p1.y - p0.y ) / ( p1.x - p0.x );	
}

which is really helpful in some cases.
this snippet determines if the line going through 2 points is ascending or descending.

private function findSlope():void 
{
	var c:Point = new Point( stage.stageWidth * .5, stage.stageHeight * .5 );
	var p:Point = new Point( stage.mouseX, stage.mouseY );
	
	var slope:Number = slope( c, p );
	
	var color:uint = ( slope > 0 ) ? 0xFF0000 : ( ( slope == 0 ) ? 0x0000FF : 0x00FF00 );
	graphics.clear();
	graphics.lineStyle( 0, color );
	graphics.moveTo( c.x, c.y );
	graphics.lineTo( p.x, p.y );
}

available here on wonderfl.
without the slope, we’d compute an angle and check wether it’s positive or negative. this, is way cheaper in computation.

that’s about all the properties of the line we can use for now ; it has an infinite length, no direction there’s not much to do with it as such. we’ll come back to it later in the polygon section.
yet as mentionned in the diagram above, 2 points define a segment and this is really a weapon of choice for us generative artist wannabes.

a segment has a slope but also a direction ( A->B or B->A ), an angle ( A^B != B^A ) and a length ( constant in both cases ) computed as follow

the direction given by how the points are stored in the data structure, it can have a great impact on how variables should be stored, especially in 3D (to determine wether a face is visible).

for the angle between A and B, we do something like:

static public function angle( p0:Point, p1:Point ):Number
{
	return Math.atan2( p1.y - p0.y, p1.x - p0.x );
}

that’s about it, the result is returned in radians, usually we don’t need degrees.

distance is a very very very very very useful data, unfortunately, it is pretty heavy to process because of the square root involved.
that’s why we may want to compute a squared distance first or at least separate the 2 methods. in practice, we often want to determine if 2 points are too close or too far from each other. in this case, we don’t need to know if the exact distance between points is inferior to a given radius but rather to know if the squared distance is inferior to the squared radius. it saves lots of computation :)

this will return the squared distance

static public function squareDistance( x0:Number, y0:Number, x1:Number, y1:Number ):Number
{
	var dx:Number = x0 - x1;
	var dy:Number = y0 - y1;
	return dx * dx + dy * dy;
}

and this will compute the actual distance:

static public function distance( p0:Point, p1:Point ):Number
{
	return Math.sqrt( squareDistance( p0.x, p0.y, p1.x, p1.y ) );
}

once again, if optimization is the rule, these methods should be inlined as needed.
we’ll add a couple of methods when we’ll talk about polygons, for now I’ll leave it as such and move forward to our next step: LINES!…
yeah…
I know…
you’ve already heard that :)

Tags: basics, generative, generative art, introduction, line