a short post to share 2 miscellaneous 3D lists. download the zip or read further.

I started reading a book called Advanced Graphics Programming Using OpenGL, very instructive even though I can’t get everythign I read.
at some point they review a couple of materials used in 3D.
I never found such a table so, despite the fact that I could have browsed and saved all the 3DSMAX default material settings, instead I isolated this table and made a html page out of it. I hope they won’t sue me for that, if need be, I’ll remove the page and apologize.

so here’s a list of parameters for some materials in 3D : http://www.barradeau.com/nicoptere/dump/materials.html
at the top of the page is a table of indices of refraction. most 3D engines can’t handle caustics so it’s of little use but who knows … :)
then you have the actual properties, for instance Emerald goes like:

the ambient, diffuse and specular settings are normalized series of values in the RGBA format. the shininess is a value comprised between 0 and 100.

could be useful.

now another thing I found is a list of the putatively optimal coverings of the sphere with n equal caps in human being terms, it’s a list of almost “perfect” ( = equidistant) distributions of N points on a sphere, the list covers distributions from 4 to 130.

Alan Shaw discovered a method that allows you to compute an arbitrary number of points and distribute them over a sphere, the only problem with that is it is emerging ; you’ll have to run the algo for some time before finding an optimal solution.

with the list, you can lookup the location of say 42 point, copy, paste, bam.
well, in fact not bam yet ; trying to tesselate the triangles might give you this:

fortunately, a sphere is by definition a convex hull, so we can use the previous article’s method to compute the indices and get then nicely sorted.

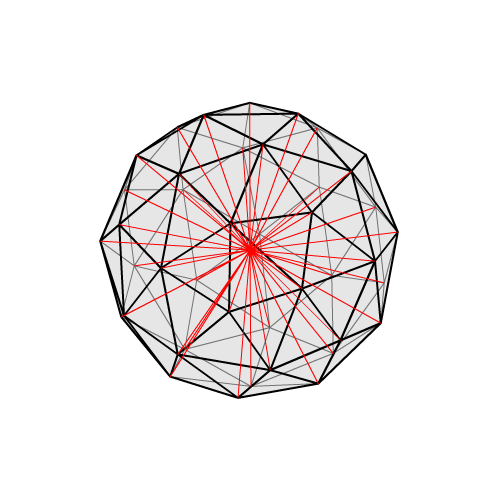
so that’s what a 42 points sphere looks like.
and this is a 130 points:

the list is here: list of perfect distributions of 4 to 130 points on a sphere

here’s a sample code to display one of the lists.
I haven’t tried them all but I trust the authors :)

private var unprojected:Vector.<Number> = new Vector.<Number>();
private var vertices:Vector.<Number> = new Vector.<Number>();
private var uvts:Vector.<Number> = new Vector.<Number>();
private var points:Vector.<Vector3D> = new Vector.<Vector3D>();
private var indices:Vector.<int> = new Vector.<int>();
private var m:Matrix3D = new Matrix3D();

public function SphereTest() 
{
	
	points = new Vector.<Vector3D>();
	
	var size:Number = 150;
	
	var positions:Vector.<Number> = Vector.<Number>( [ /*
	copy paste a list from:

http://www.barradeau.com/nicoptere/dump/sphere_distributions.html

														*/ ] );
	
	for ( var i:int = 0; i < positions.length; i+=3 )
	{
		points.push( new Vector3D( 	positions[ i ] * size, 
									positions[ i + 1 ] * size, 
									positions[ i+2 ] * size ) );
	}
	
	//processing the convex hull
	indices = ConvexHull.process( points );
	
	for each ( var v:Vector3D in points )
	{
		unprojected.push( v.x, v.y, v.z );
	}
	
	x = y = 250;
	addEventListener( Event.ENTER_FRAME, render );
	
}

private function render( e:Event ):void
{
	graphics.clear();
	
	m.prependRotation( .1, Vector3D.Y_AXIS );
	Utils3D.projectVectors( m, unprojected, vertices, uvts );
	
	if ( indices != null )
	{
		graphics.lineStyle( 0, 0, .5 );
		graphics.drawTriangles( vertices, indices, null, TriangleCulling.NEGATIVE );
		graphics.lineStyle( 2 );
		graphics.drawTriangles( vertices, indices, null, TriangleCulling.POSITIVE );
	}
	
}

pretty convenient if you have to distribute a given amount of objects on 3D a sphere :)
and in case you want to refine ( subdivide the sphere ), here’s a method to do that.

private function refine(points:Vector.<Vector3D>, indices:Vector.<int>, iterations:int = 1, max:int = 0 ):void 
{
	var tmp:Vector.<int> = new Vector.<int>();
	
	var v:Vector3D = points[ 0 ];
	var radius:Number = Math.sqrt( v.x * v.x + v.y * v.y + v.z * v.z );
	
	var v0:Vector3D, v1:Vector3D, v2:Vector3D;
	var total:int = indices.length;
	var i0:int, i1:int, i2:int, i3:int, i4:int, i5:int;
	
	for ( var i:int = 0; i < total; i+=3 )
	{
		v0 = points[ i0 = indices[ i ] ];
		v1 = points[ i1 = indices[ i + 1 ] ];
		v2 = points[ i2 = indices[ i + 2 ] ];
		
		i3 = points.length;
		points.push( midVector( v0, v1, radius ) );
		
		i4 = points.length;
		points.push( midVector( v1, v2, radius ) );
		
		i5 = points.length;
		points.push( midVector( v2, v0, radius ) );
		
		tmp.push( 
				i0, i3, i5, 
				i1, i4, i3, 
				i2, i5, i4, 
				i3, i4, i5
				);
		
	}
	for ( i = 0; i < tmp.length; i++ )
	{
		indices[ i ] = tmp[ i ];
	}
	if ( iterations < max )
	{
		iterations++;
		refine( points, indices, iterations, max );
	}
}
private function midVector(v0:Vector3D, v1:Vector3D, radius:Number ):Vector3D 
{
	var v:Vector3D = new Vector3D( 	v0.x + ( v1.x - v0.x ) * .5,
									v0.y + ( v1.y - v0.y ) * .5,
									v0.z + ( v1.z - v0.z ) * .5		);
	v.normalize();
	v.scaleBy( radius );
	return v;
}

this will take each face, create 3 new vertices per face and 4 new faces.
call:

refine( points, incidces, 0, 3 );

after having created the indices to perform the subdivision.
warning, this does not eliminate duplicate vertices so you”l end up having a consequent amount of vertices/face.
here’s what you’d get when refining 4 a sphere made of 7 vertices:

10237 vectors and 10240 faces.

Tags: 3D, sphere, texture