I just came back from Lisbon, each and every friend of mine told me about a very enjoyable place with lovely people, none of them – fools ! – told me about Azulejos.
when I unknowingly found the first wall covered with them, I thought it was some fancy pants landlord trying to show off, but after passing in front of dozens of them, covering houses that didn’t seem especially wealthy, I started realizing that it was a widespread and much alive form of art. Azulejos admittedly reached their finest expression in Portugal, Lisbon therefore became a playground and I started hunting them in the city.
I am fascinated by islamic patterns, a couple of years ago I tried to understand the regular patterns, which describe the sets of operations used to cover planar surfaces with repetitive sets of items.
there are 3 groups of regular patterns. they are called after the number and the type of operations that are performed on the fundamental region:
the 1,2,3,4,6 is the number of operations and very often, the number of rotations, t stands for Translation, m for Mirror or Reflection, g for Glide, p would be the prefix for the Plane group, and sometimes you get a c ; it’s a staggered version of m, used only in the plane group.
so we can use this set of operations to create patterns and friezes: 1, m, 2, 2mm, 3, 3m, 4, 4mm, 6, 6mm t, tg, tm, mt, t2, t2mg, t2mm and this set to tile the plane: p1, p2, pm, pg, cm, p2mm, p2mg, p2gg, c2mm, p3, p3m1, p31m, p4, p4mm, p4gm, p6, p6mm
azulejos use very simple transformations, mostly rotations around a lattice and translations along with friezes (the lines group). that’s the first picture I took

you can clearly see that the central tile is the only thing we need to create the whole pattern.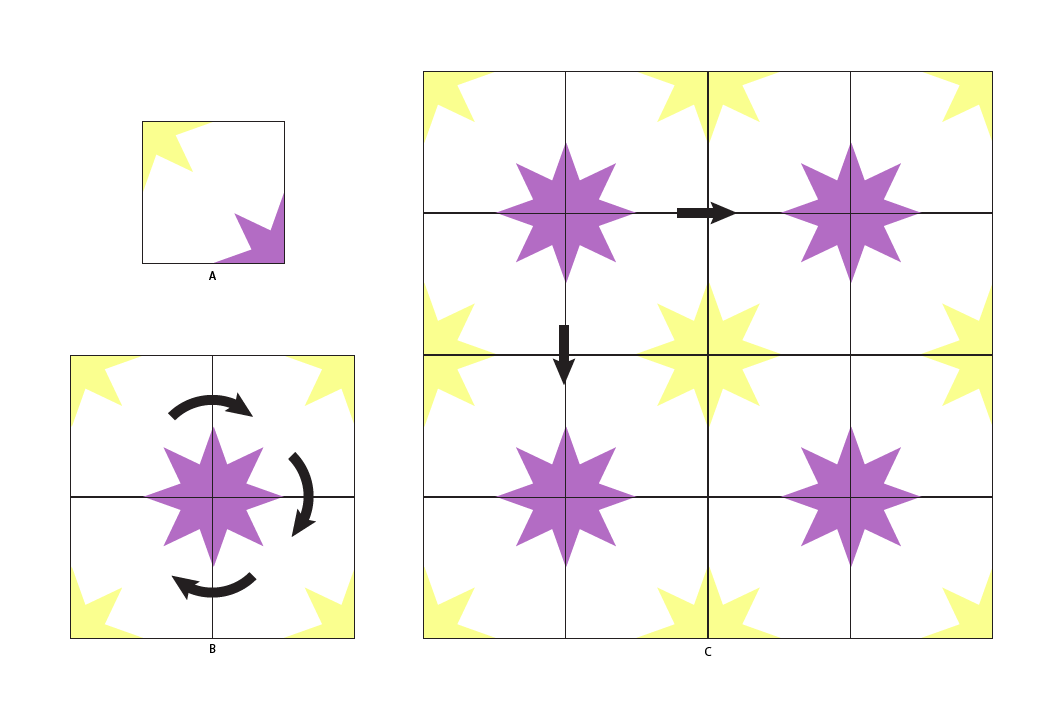
with a fundamental region (A) the first operation is a 4 point rotation around one of the lattices (B), this builds a unit cell that is then used with a P1 transform (C) to cover a plane. note that if the feature region is the unit cell, this is the P4 plane tiling.
the reason why transformations are rather simple is probably that producing actual tiles is more costly than drawing patterns on paper or with a computer. a reflection for instance means that you’ll end up with 2 sets of different tiles, some of which may not be used as much as the other, or the workers would mistake the patterns as it’s really hard to tell some patterns apart when they’re just reflected.
if we don’t use reflection, all the tiles will work interchangeably as only one type of tile is required. with a single tileset, the designs can’t use the following transformations: m, 2mm, 3m, 4mm, 6mm, tg, tm, mt, t2mg, t2mm, pm, pg, cm, p2mm, p2mg, p2gg, c2mm, p3m1, p31m, p4mm, p4gm, p6mm which – theoretically – leaves us with: 1, 2, 3, 4, 6, t, t2, p1, p2, p3, p4, p6 but as the tiles are square (or rectangles for the friezes), we can only use rotations of 90° or 180° for the friezes. the same goes for planar tilings ; P2 for instance uses a triangular unit cell which is not compatible with square tiles. removing the impossible settings boils the list down to these 7 settings: 1, 2, 4, t, t2, p1, p4.
it might seem few but while the tiles’ distribution must obey some strict and limited rules, the tiles themselves can exhibit the most intricate patterns and complex symmetries.
and of course there are exceptions! this one for instance

it belongs to the CM plane group, there is no way to obtain this pattern if you don’t produce a mirrored set of the original tile.

on a side note: this specific tileset – like many others in the Alfama – was hand-painted, you can see the brush stroke, the variation in the pigment distribution, the little mistakes done when copying the original pattern like stroke-width variation, clumsy, unfinished strokes, etc. my love I love is an illustrator, and I think we – she drew a whole set of those – spent a good 30 minutes staring at this wall and locals must have (rightfully) thought we were crazy.
this specimen is mind boggling and it’s (by far) the more complex I found, this is the lower right part of it.
 it’s made of 43 unique tiles:
it’s made of 43 unique tiles:
- the center tile (top left) is horizontally and vertically symmetric
- 2*3 tiles are axially symmetric (top row, horizontally & left column, vertically) so they can be reused twice
- 4*9 tiles (the 9 of the bottom right corner) have to be mirrored 4 times, once for each quadrant
each tile is hand-painted, this is almost a mural (there are many sophisticated murals made of tiles in Lisbon). more recent azulejos seem to be silk-screen printed,they are more complex, more regular but also less moving in a way.
just before I left, I received a new mobile phone, a samsung S6, and it felt like entering the future ; not only could I take pictures and videos with decent resolutions but I could finally use GPS tags. I thought it would be interesting to map the various areas where I took pictures, just to see if a pattern or some kind of spatial relation would emerge.
So I extracted the GPS coordinates of my pictures using this handy JS lib Exif.js which provides the data as Degrees Minutes Seconds like so
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
var img = new Image(); img.onload = function(e){ EXIF.getData( img, function() { var tags = EXIF.getAllTags( img ); if( tags.GPSLatitude != null && tags.GPSLongitude != null ){ var latsign = 1; if( tags.GPSLatitudeRef.charCodeAt(0) == "S".charCodeAt(0) ) latsign = -1; var lngsign = 1; if( tags.GPSLongitudeRef.charCodeAt(0) == "W".charCodeAt(0) ) lngsign = -1; var dtd = degreesToDecimal( parseFloat( tags.GPSLatitude[0] ) * latsign, parseFloat( tags.GPSLatitude[1] ), parseFloat( tags.GPSLatitude[2] ), parseFloat( tags.GPSLongitude[0] ) * lngsign, parseFloat( tags.GPSLongitude[1] ), parseFloat( tags.GPSLongitude[2] ) ); lat = dtd[0]; lng = dtd[1]; coords.push( [img.src, lat, lng] ); } }); }; img.src = "yourpic.jpg"; |
the DMS to decimal values is done using this handy script. from which I got this method
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
function degreesToDecimal( dlat, mlat, slat, dlon, mlon, slon ){ var latsign = dlat < 0 ? - 1 : 1; var lonsign = dlon < 0 ? - 1 : 1; absdlat = Math.abs( Math.round(dlat * 1000000.)); mlat = Math.abs(Math.round(mlat * 1000000.)/1000000); absmlat = Math.abs(Math.round(mlat * 1000000.)); slat = Math.abs(Math.round(slat * 1000000.)/1000000); absslat = Math.abs(Math.round(slat * 1000000.)); absdlon = Math.abs( Math.round(dlon * 1000000.)); mlon = Math.abs(Math.round(mlon * 1000000.)/1000000); absmlon = Math.abs(Math.round(mlon * 1000000)); slon = Math.abs(Math.round( slon * 1000000.)/1000000); absslon = Math.abs(Math.round( slon * 1000000.)); alat = Math.round(absdlat + (absmlat/60.) + (absslat/3600.) ) * latsign/1000000; alon = Math.round(absdlon + (absmlon/60) + (absslon/3600) ) * lonsign/1000000; return [ alat,alon ]; } |
I fed this to my map API using the Stamen Toner tileset which gave me a first idea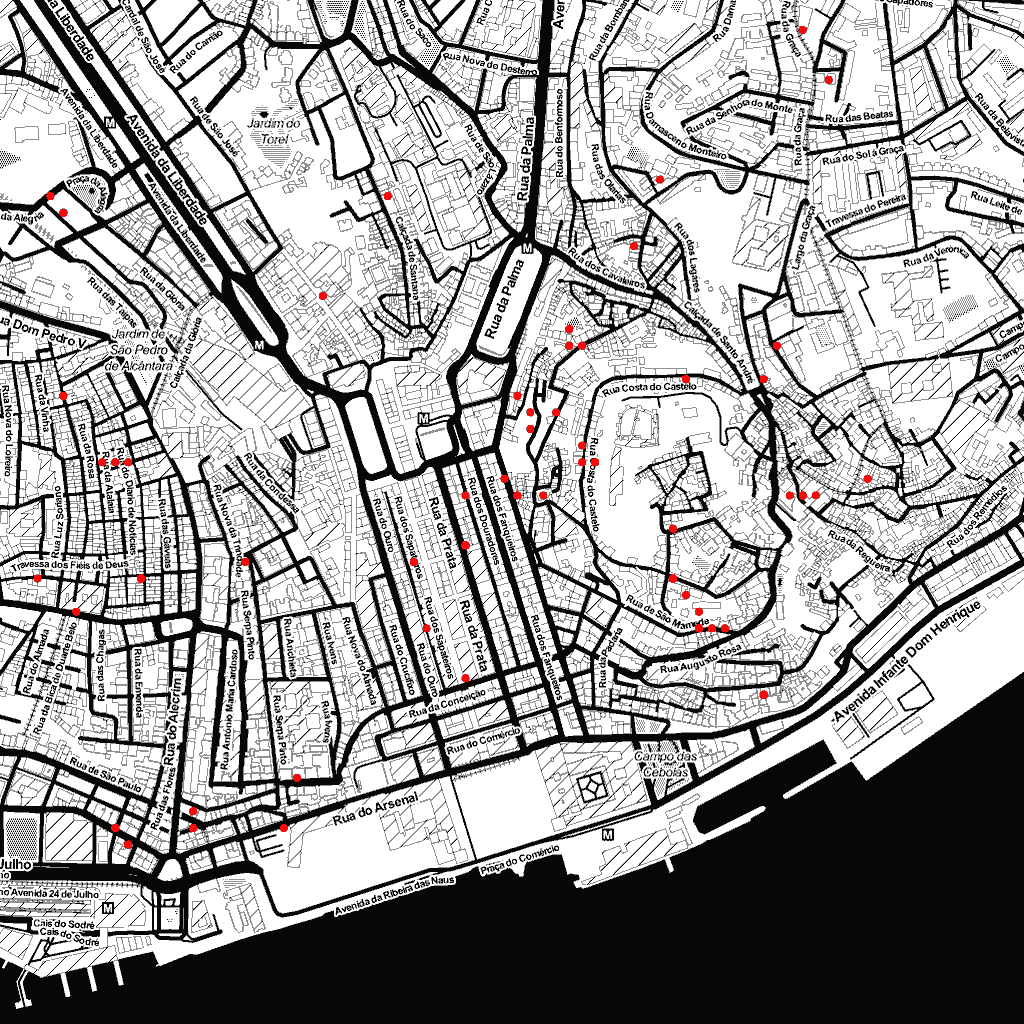 if you’ve ever been to Lisbon, the distribution won’t be much of a surprise ; that’s the tourist area :)
if you’ve ever been to Lisbon, the distribution won’t be much of a surprise ; that’s the tourist area :)
then I wondered what the “influence zone” of each azulejo would look like. I first computed the Voronoi diagram of the point set using this lib which gave this map (interactive)
finally I wanted a kind of mosaic of patterns so I created a texture of all the pictures I had
and used it to paint the voronoi cells with their own texture to obtain this interactive mosaic
here are some screenshots in case the demo is broken
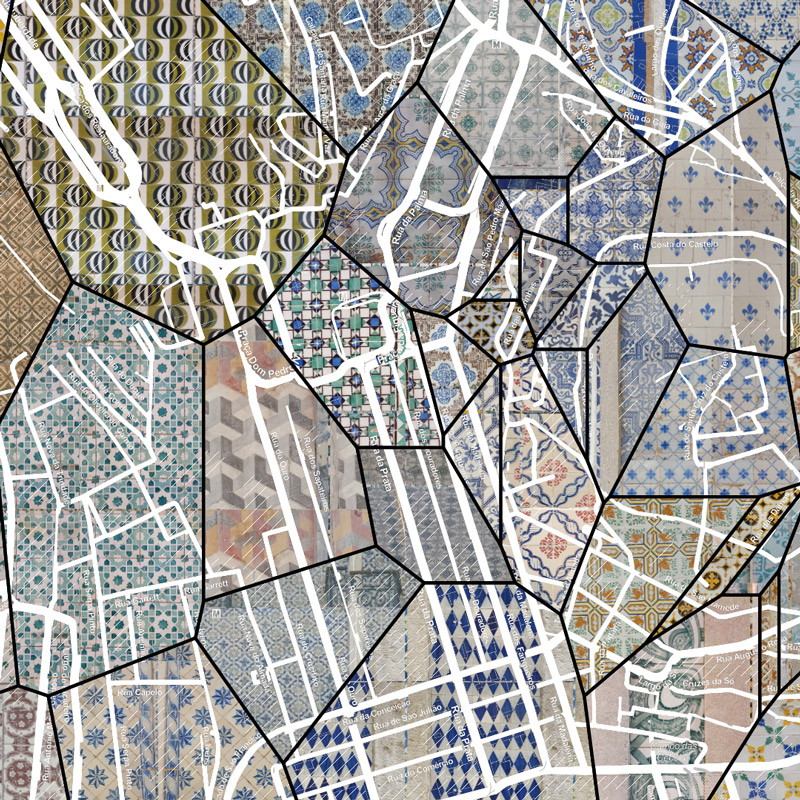
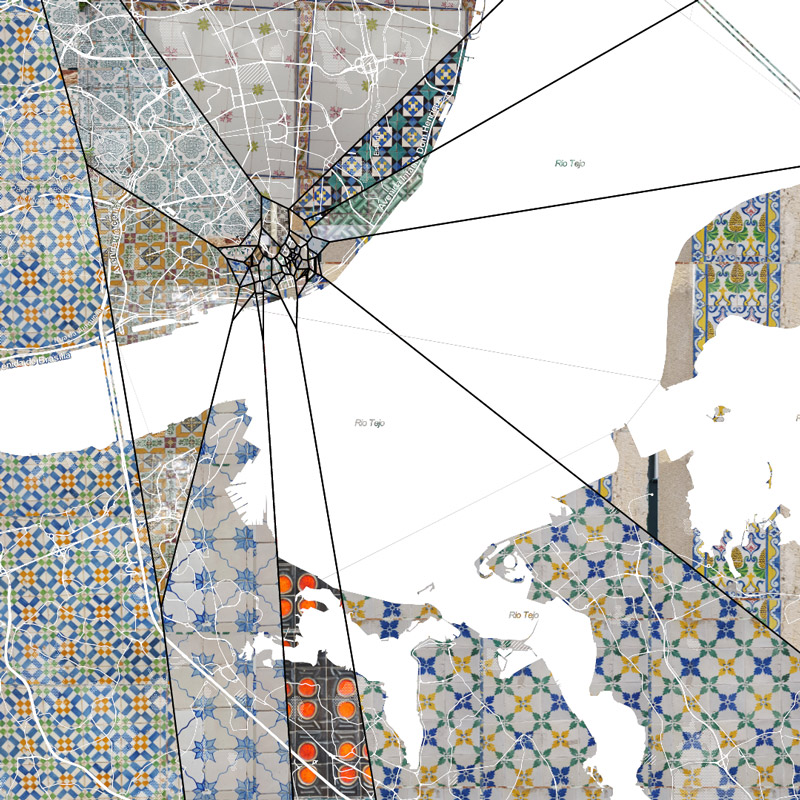 lovely ain’t it? actually I thought an overall pattern would emerge but no luck, or maybe there is something obvious and I don’t know enough of Lisbon’s history/culture to read it. anyway this helped me understand that 74 pictures is way too few to meaningfully represent anything of a city, at least it was a fun little exercise :)
lovely ain’t it? actually I thought an overall pattern would emerge but no luck, or maybe there is something obvious and I don’t know enough of Lisbon’s history/culture to read it. anyway this helped me understand that 74 pictures is way too few to meaningfully represent anything of a city, at least it was a fun little exercise :)

maybe they are defined by what nearest shop sells.