marching squares

a short post about the marching squares algorithm, a technique mostly used to vectorize the outline of a binary image.

it’s a very well known & very well spread technique, I happened to have some spare time & the urge to do something graphic.
for a start let’s look at how things work.

the idea is to draw a shape through the edges of cells which vertices are “weighted” ( each point of the cell has a value ). in our case, we use an image to represent the cells’ grid ( an image is a grid of pixels ) & if we use a binary image (black & white, no greyscale), the weights are the colors of the pixels ( 0 or 1 ) . then we need a structuring element or kernel to scan our grid & find the outline.

the algorithm goes as follow:

apply a threshold to the image to obtain a binary image
find the first non transparent pixel
position the kernel at this location
while the kernel has not reached the starting location
- move the kernel around the shape
- store the new location
- if the number of iteration is too high, break
- else continue

the first step is fairly easy ; when you access the imageData of a given canvas, you can scan all the pixels’ components ( r,g,b or a ) & match them against a given value.

a good idea though is to reduce the image’s colors before performing the marching square process ; this can be done quite simply either beforehand by using a restricted palette or on the fly by applying a simple reduction algorithm like:

function segment( imageOrCanvas, steps )
{

    var w = imageOrCanvas.width;
    var h = imageOrCanvas.height;
    var canvas = document.createElement("canvas");
    document.body.appendChild( canvas );
    canvas.width = w;
    canvas.height = h;

    var context = canvas.getContext("2d");
    context.fillStyle = "rgba(255,255,255,255)";
    context.fillRect(0, 0, w, h);
    context.drawImage(imageOrCanvas, 0, 0 );

    var imgData = context.getImageData(0, 0, w, h);
    var data = imgData.data;

    for( var i = 0; i < data.length; i += 4 )
    {
        data[i]     = parseInt(parseInt( ( data[i] / 0xFF ) * steps + .5 ) * ( 0xFF / steps ) );
        data[i + 1] = parseInt(parseInt( ( data[i + 1] / 0xFF ) * steps + .5 ) * ( 0xFF / steps ) );
        data[i + 2] = parseInt(parseInt( ( data[i + 2] / 0xFF ) * steps + .5 ) * ( 0xFF / steps ) );
    }

    imgData.data = data;
    context.putImageData( imgData, 0, 0 );

}
var img = document.getElementById( "me_gusta" );
segment( img, 16 );
segment( img, 8 );
segment( img, 1 );

function segment( imageOrCanvas, steps )

{

var w = imageOrCanvas.width;

var h = imageOrCanvas.height;

var canvas = document.createElement("canvas");

document.body.appendChild( canvas );

canvas.width = w;

canvas.height = h;

var context = canvas.getContext("2d");

context.fillStyle = "rgba(255,255,255,255)";

context.fillRect(0, 0, w, h);

context.drawImage(imageOrCanvas, 0, 0 );

var imgData = context.getImageData(0, 0, w, h);

var data = imgData.data;

for( var i = 0; i < data.length; i += 4 )

{

data[i] = parseInt(parseInt( ( data[i] / 0xFF ) * steps + .5 ) * ( 0xFF / steps ) );

data[i + 1] = parseInt(parseInt( ( data[i + 1] / 0xFF ) * steps + .5 ) * ( 0xFF / steps ) );

data[i + 2] = parseInt(parseInt( ( data[i + 2] / 0xFF ) * steps + .5 ) * ( 0xFF / steps ) );

}

imgData.data = data;

context.putImageData( imgData, 0, 0 );

}

var img = document.getElementById( "me_gusta" );

segment( img, 16 );

segment( img, 8 );

segment( img, 1 );

which will give you something like

the idea is simple, for each component of the color, first normalize it ( data[ X ] / 0xFF ) then interpolate between 0 & the desired amount of steps ( * steps ) & Math.ceil it ( parseInt( X + .5 ) ) then multiply this by the value of a color step ( 0xFF / steps ).

the lower the number of steps, the easier it should be to vectorize, adding a blur step before reduces the noise & gives more usable regions.

to understand what comes next, you may need to understand the notion of kernel but there’s this example by Sakri that shows exactly what the last step of the algorithm is about: http://codepen.io/sakri/pen/aIirl

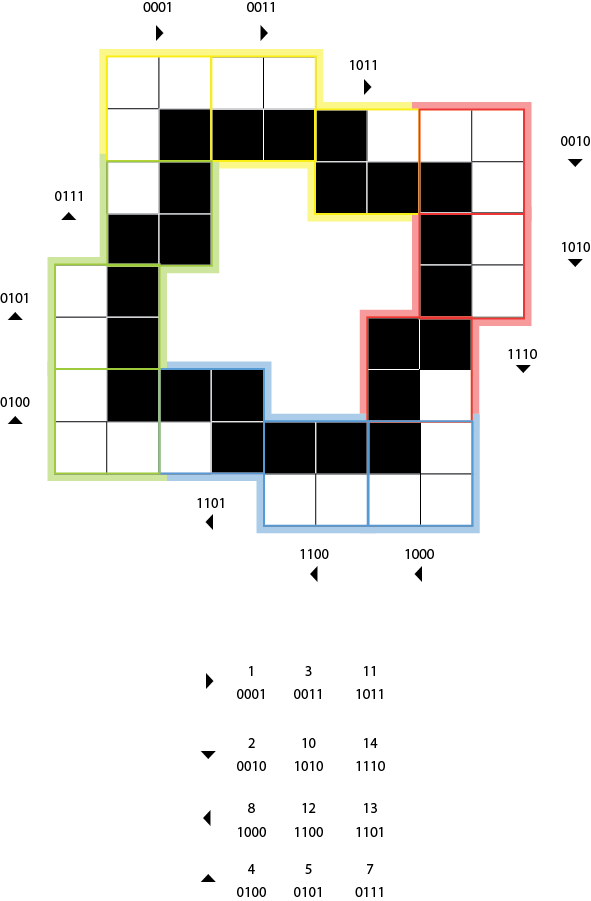
as we’re using a simple 2 * 2 kernel, there are very few possibilities ( only 16 actually ) to move the kernel when looking for the direction. here’s a table with the integers 0-15 in binary form, the 4 rectangles below the figure represent the bytes ( white=0, black = 1 ) & the squares are the kernel itself ; what we’ll use to actually determine the direction to move to (represented by the arrow above the box).

by sampling the right, bottom & bottom right pixels, this table allows us to quickly determine where we should go next but there are 2 flaws.

a minor flaw is that it contains both a 2 * 2 void square ( 0000 ) and a 2 * 2 full square ( 1111 ). this is not that bad ; as we select the first non-transparent pixel, it is usually located on the top left area of the picture so 0000 will head towards the bottom right & 1111 will head towards the top left.

the second flaw is more embarrassing though, it rises about the values 6 ( 0110 ) & 9 ( 1001 ) and form a diagonal pattern. in these cases, there is no way to tell where to send the kernel next, ending up in infinite loops. there are ways to deal with this problem but that’s beyond the scope of this article.

to prevent the infinite loops, I tried simply not to use those patterns.

which failed of course.

but it gave me an idea ; why not alter the binary shape so that this pattern doesn’t occur?

enter the Morphological operators.
the morphological operators work on binary images & perform very simple tests between a pixel & its neighborhood to determine whether or not to toggle a pixel.

this simple operators fill the smaller gaps that cause most of the infinite loops and applying this during the collection phase ( step 1 of the algorithm ) allows for not having to bother with ambiguous case anymore.

let’s take this burning head I did so it has a fair amount of ambiguous cases (click to view full size) especially in the bottom right corner.

trying a brute force marching square will fail, but applying the following kernel:

buffer[ id ] = 0;
if (sum != 9 && sum > 1 )
{
    buffer[ id ] = 1;
}

//then 
if( sum > dilation )//dilation default: 5, lower = more greedy
{
    buffer[ i ] = 1;
}

buffer[ id ] = 0;

if (sum != 9 && sum > 1 )

{

buffer[ id ] = 1;

}

//then

if( sum > dilation )//dilation default: 5, lower = more greedy

{

buffer[ i ] = 1;

}

where sum is the sum of the neighboring pixels’ values, allows to preserve only the outline of the shape and gives the red outline (click to view full size)

if you look closely, you can follow the whole border without finding any ambiguous case + smaller elements (namely single pixels) are being discarded. now instead of 16 possibilities, we end up managing only 12 the Lookup table now looks like this:

the burning head vectorized output looks like this

the blue area is the vectorized outline and the orange line & dots is the simplified version of the path. nice isn’t it?

here’s the code of the marching squares method:

/**
 * function that performs a marching squares vectorization
 * @param imageOrCanvas an image or a canvas to vectorize, preferably a binary image.
 * @param color the color you want to vectorize ( between 0 & 0xFFFFFF )
 * @param dilation value used in the dilation step ( 0 - 8 )
 * @param maxIterations this prevents infinte loops ( default 10e5 )
 * @returns {Array} a series of x, y coordinates
 * @constructor
 */
function MarchingSquares( imageOrCanvas, color, dilation, maxIterations )
{

    dilation = dilation == null ? 5 : dilation;

    maxIterations = maxIterations == null ? 10e5 : maxIterations;

    var canvas = document.createElement( "canvas" );
    var w = canvas.width = imageOrCanvas.width + 4;
    var h = canvas.height = imageOrCanvas.height + 4;

    var context = canvas.getContext("2d");
    context.fillStyle = "rgba(255,255,255,255)";
    context.fillRect( 0,0, w, h );
    context.drawImage( imageOrCanvas, 2, 2 );

    var imgData= context.getImageData( 0,0,w,h );
    var data = imgData.data;
    var buffer = new Int8Array(w*h);
    var path = [];
    var first = NaN;

    var i;
    var r = color >> 16  & 0xFF;
    var g = color >> 8  & 0xFF;
    var b = color  & 0xFF;

    for( i = 0; i < data.length; i+=4 )
    {
        // discard if the pixel has a different
        // color than what we're looking for
        if( data[ i ]       != r
        &&  data[ i + 1 ]   != g
        &&  data[ i + 2 ]   != b )
        {
            data[ i + 3 ] = 0;
        }
        else
        {
            data[ i + 3 ] = 1;
        }
    }

    //morphological operation extracting the border
    for( i = 0; i < data.length; i+=4 )
    {
        id = i / 4;
        var sum = neighborSum( data, i, 4, 3 );

        buffer[ id ] = 0;
        if (sum != 9 && sum > 1 )
        {
            buffer[ id ] = 1;
        }
    }

    //morphological dilation
    //this prevents infinite loops
    for( i = 0; i < buffer.length; i++ )
    {

        sum = neighborSum( buffer, i, 1, 0 );
        if( sum > dilation )
        {
            buffer[ i ] = 1;
        }

        // first non transparent pixel ( top left to current pixel )
        if( isNaN( first ) && buffer[ i  ] == 1 )
        {
            first = i - w - 1;
        }
    }

    if( isNaN( first ) )
    {
        console.log( "warning: no empty pixels was found, exiting." );
        return [];
    }

    //morphological operators

    function neighborIds( id, stride )
    {
        stride = stride || 1;

        var to = id - w * stride;//top
        var tr = to + stride;//top right
        var tl = to - stride;//top left

        var ri = id + stride; // right
        var le = id - stride;//left

        var bo = id + w * stride;//bottom
        var br = bo + stride;//bottom right
        var bl = bo - stride;//bottom left

        return [ tl, to, tr, le, id, ri, bl, bo, br ];
    }

    function neighborValues( data, id, stride, offset )
    {
        var values = [];
        var ids = neighborIds( id, stride );
        ids.forEach( function( id )
        {
            values.push( data[ id + offset ] );
        });
        return values;
    }

    function neighborSum( data, id, stride, offset )
    {
        var values = neighborValues( data, id, stride, offset );
        var sum = 0;
        values.forEach( function( value )
        {
            sum += ( value > 0 ) ? 1 : 0;
        });
        return sum;
    }

    //marching square

    var iteration = 0;
    var id = getDirection( buffer, first );
    while( iteration++ < maxIterations )
    {
        id = getDirection( buffer, id );

        path.push( id % w - 1, parseInt( id / w ) - 1 );

        if( id == first )    break;//done
    }

    //determine where to move next
    function getDirection( data, id  )
    {

        var ri  = id + 1;// right pixel
        var bo  = id + w;//bottom pixel
        var br = bo + 1;//bottom right pixel

        var x = 0;
        var y = 0;
        var key = data[ id ] << 3 | data[ ri ] << 2 | data[ bo ] << 1 | data[ br ];

        if( key == 1 || key ==  3 || key == 11  ) x =  1;// rightt
        if( key == 8 || key == 12 || key == 13  ) x = -1;// left
        if( key == 4 || key ==  5 || key ==  7  ) y = -1;// up
        if( key == 2 || key == 10 || key == 14  ) y =  1;// down

        return id + x + y * w;

    }
    return path;
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

/**

* function that performs a marching squares vectorization

* @param imageOrCanvas an image or a canvas to vectorize, preferably a binary image.

* @param color the color you want to vectorize ( between 0 & 0xFFFFFF )

* @param dilation value used in the dilation step ( 0 - 8 )

* @param maxIterations this prevents infinte loops ( default 10e5 )

* @returns {Array} a series of x, y coordinates

* @constructor

function MarchingSquares( imageOrCanvas, color, dilation, maxIterations )

{

dilation = dilation == null ? 5 : dilation;

maxIterations = maxIterations == null ? 10e5 : maxIterations;

var canvas = document.createElement( "canvas" );

var w = canvas.width = imageOrCanvas.width + 4;

var h = canvas.height = imageOrCanvas.height + 4;

var context = canvas.getContext("2d");

context.fillStyle = "rgba(255,255,255,255)";

context.fillRect( 0,0, w, h );

context.drawImage( imageOrCanvas, 2, 2 );

var imgData= context.getImageData( 0,0,w,h );

var data = imgData.data;

var buffer = new Int8Array(w*h);

var path = [];

var first = NaN;

var i;

var r = color >> 16 & 0xFF;

var g = color >> 8 & 0xFF;

var b = color & 0xFF;

for( i = 0; i < data.length; i+=4 )

{

// discard if the pixel has a different

// color than what we're looking for

if( data[ i ] != r

&& data[ i + 1 ] != g

&& data[ i + 2 ] != b )

{

data[ i + 3 ] = 0;

}

else

{

data[ i + 3 ] = 1;

}

//morphological operation extracting the border

for( i = 0; i < data.length; i+=4 )

{

id = i / 4;

var sum = neighborSum( data, i, 4, 3 );

buffer[ id ] = 0;

if (sum != 9 && sum > 1 )

{

buffer[ id ] = 1;

}

//morphological dilation

//this prevents infinite loops

for( i = 0; i < buffer.length; i++ )

{

sum = neighborSum( buffer, i, 1, 0 );

if( sum > dilation )

{

buffer[ i ] = 1;

}

// first non transparent pixel ( top left to current pixel )

if( isNaN( first ) && buffer[ i ] == 1 )

{

first = i - w - 1;

}

if( isNaN( first ) )

{

console.log( "warning: no empty pixels was found, exiting." );

return [];

}

//morphological operators

function neighborIds( id, stride )

{

stride = stride || 1;

var to = id - w * stride;//top

var tr = to + stride;//top right

var tl = to - stride;//top left

var ri = id + stride; // right

var le = id - stride;//left

var bo = id + w * stride;//bottom

var br = bo + stride;//bottom right

var bl = bo - stride;//bottom left

return [ tl, to, tr, le, id, ri, bl, bo, br ];

}

function neighborValues( data, id, stride, offset )

{

var values = [];

var ids = neighborIds( id, stride );

ids.forEach( function( id )

{

values.push( data[ id + offset ] );

});

return values;

}

function neighborSum( data, id, stride, offset )

{

var values = neighborValues( data, id, stride, offset );

var sum = 0;

values.forEach( function( value )

{

sum += ( value > 0 ) ? 1 : 0;

});

return sum;

}

//marching square

var iteration = 0;

var id = getDirection( buffer, first );

while( iteration++ < maxIterations )

{

id = getDirection( buffer, id );

path.push( id % w - 1, parseInt( id / w ) - 1 );

if( id == first ) break;//done

}

//determine where to move next

function getDirection( data, id )

{

var ri = id + 1;// right pixel

var bo = id + w;//bottom pixel

var br = bo + 1;//bottom right pixel

var x = 0;

var y = 0;

var key = data[ id ] << 3 | data[ ri ] << 2 | data[ bo ] << 1 | data[ br ];

if( key == 1 || key == 3 || key == 11 ) x = 1;// rightt

if( key == 8 || key == 12 || key == 13 ) x = -1;// left

if( key == 4 || key == 5 || key == 7 ) y = -1;// up

if( key == 2 || key == 10 || key == 14 ) y = 1;// down

return id + x + y * w;

}

return path;

}

it’s intentionally unoptimized for legibility but one would probably merge & inline the morphological operator, unfold & reorganize the way getDirection sets the x/y directions, reuse the canvas & the buffer instead of recreating it a.s.o.

and a standard call would go like :

function sample( img )
{

    var out = document.createElement( "canvas" );
    out.width = img.width;
    out.height = img.height;
    document.body.appendChild( out );

    var out_context = out.getContext("2d");
    out_context.drawImage( img,0,0,out.width, out.height );

    var path = MarchingSquares( img, 0, 5, 10e5 );

    out_context.fillStyle = "rgba( 255,0,0,.35 )";
    out_context.strokeStyle = "rgba( 255,0,0, .7 )";
    out_context.lineWidth = 3;
    out_context.beginPath();

    for( var i = 0; i < path.length; i+=2 )
    {
        out_context.lineTo( path[ i ], path[ i+1 ] );
    }
    out_context.closePath();
    out_context.stroke();
    out_context.fill();

}

window.onload = function()
{
    var img = document.getElementById( "my_favorite_unicorn" );
    sample( segment( img,1 ) );
};

function sample( img )

{

var out = document.createElement( "canvas" );

out.width = img.width;

out.height = img.height;

document.body.appendChild( out );

var out_context = out.getContext("2d");

out_context.drawImage( img,0,0,out.width, out.height );

var path = MarchingSquares( img, 0, 5, 10e5 );

out_context.fillStyle = "rgba( 255,0,0,.35 )";

out_context.strokeStyle = "rgba( 255,0,0, .7 )";

out_context.lineWidth = 3;

out_context.beginPath();

for( var i = 0; i < path.length; i+=2 )

{

out_context.lineTo( path[ i ], path[ i+1 ] );

}

out_context.closePath();

out_context.stroke();

out_context.fill();

}

window.onload = function()

{

var img = document.getElementById( "my_favorite_unicorn" );

sample( segment( img,1 ) );

};

for instance calling this on a unicorn picture would give this kind of output

one of the greatest benefits of vectorization being to make images scale-free, my favourite results come from smaller images ; here are 2 32 * 32 pictures vectorized & simplified:

that’s far from bulletproof and I wouldn’t recommend using it in production but that’s a fun little algorithm to play with. it allows on the fly vectorization of free shapes to use in physics games for instance.

possible enhancements include, multiple shapes vectorization & triangulation, using better interpolation techniques than binary, using integral images (?!) also, I’d recommend reading this lovely article: Metaballs and marching squares by Jamie Wong.

that was it!

enjoy :)

Youpi !

marching squares

One Comment

Leave a Reply Cancel reply