I’m trying to get a proper quilting algorithm to work, one of the important steps is to cleverly “cut” a portion of the image that is going to be drawn on top of another. so I was thinking of how I’d work around this and came up with something I thought was worth sharing.
the idea is simple, find the weakest line that cuts a bitmap in two and preserve one of the halves. it’s also the idea behind an old disco number called seam carving described here and there, that kept many a flash developer busy in 2008.
to find the weak lines, we need a metric to compute the cost of a line and determine which would be the cheapest. I used the greyscale as the energy table to compute the cost of a path and an 8 pixels kernel as the neighbourhood (a very naive approach). in the case of the quilting, we always have a direction which to cut and this direction is axis aligned (up, down, left, right) a visual explanation of the algorithm would be as follow for the DOWN direction:
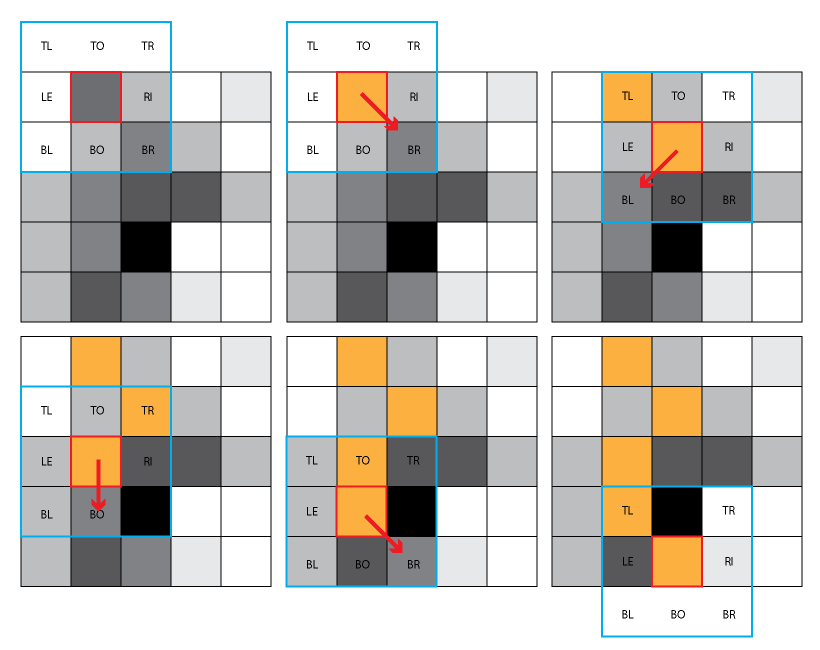1 pick the start pixel & evaluate its color (its greyscale value)
2 evaluate the neighbouring pixels’ values & choose the one with the smallest cost (the closest grey value to the current pixel), in the case of a DOWN direction, only the 3 pixels below the current pixel are necessary (BL, BO, BR), if we go to the right, only the 3 pixels to the right of the current pixel are necessary (TR, RI, BR) etc.
3 store the coordinates & move to the next location, goto 2
4,5,6 repeat 2 & 3 until you reach the bottom of the picture
this was all good but I realized that the relationships between pixels (the cost to go from one to the next) do not change from one path to the other + there are only 3 choices per direction (=2 bits) each time. this means that the 4 smallest costs could be encoded on 8 bits, stored and looked up which would probably speed up the path finding.
this is how I encode the costs in a compact format to perform quick lookups:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
//for each pixel, find the shortest energy direction to its 8 neighbours var tl, to, tr, le, ri, bl, bo, br; //pixel-neighbour distance values var vle, vto, vri, vbo; for( y = 0; y < h; y++ ) { for (x = 0; x < w; x++) { //gets the pixel greyscale value id = ( ( y * w ) + x ) * 4; v = data[id]; //greyscale values of the kernel ( top left, top, top right, left, right, bottom left, bottom, bottom right ) tl = data[ id - w4 - 4 ]; to = data[ id - w4 ]; tr = data[ id - w4 + 4 ]; le = data[ id - 4 ]; ri = data[ id + 4 ]; bl = data[ id + w4 - 4 ]; bo = data[ id + w4 ]; br = data[ id + w4 + 4 ]; //find best candidate for each direction vle = getIndex( v, tl, le, bl ); vto = getIndex( v, tl, to, tr ); vri = getIndex( v, tr, ri, br ); vbo = getIndex( v, bl, bo, br ); //4 best candidates encoded in the green channel (CW from top to left) data[ id + 1 ] = vto << exports.TOP | vri << exports.RIGHT | vbo << exports.BOTTOM | vle << exports.LEFT; } } |
a visual explanation of the last line of the loop (that bit shifts values to pack them in an 8 bits integer)
here’s the getIndex() method that determines the lowest cost between the 3 candidates (the “for each side” above):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
//return the least energy neghbour function getIndex( value, a,b,c ) { var i0 = Math.abs( value - a ); var i1 = Math.abs( value - b ); var i2 = Math.abs( value - c ); //all 3 pixels have the same value, return random index if( i0 == i1 && i1 == i2 )return parseInt( Math.random() * 3 ); //2 pixels have the same value //randomly return one of the 2 if they are lower than the third value if( i0 == i1 && i1 != i2 )return i1 < i2 ? ( ( Math.random() < .5 ) ? 0 : 1 ) : 2 ; if( i1 == i2 && i2 != i0 )return i2 < i0 ? ( ( Math.random() < .5 ) ? 1 : 2 ) : 0 ; if( i2 == i0 && i0 != i1 )return i0 < i1 ? ( ( Math.random() < .5 ) ? 2 : 0 ) : 1 ; //regular case, choose smallest difference var min = Math.min( i0, Math.min( i1, i2 ) ); if( min == i0 ) return 0; if( min == i1 ) return 1; if( min == i2 ) return 2; } |
once we have this look up table, finding the least energy path is quite trivial ; we need to look up the next pixel in the direction we’re searching, read this pixel’s value, shift and mask this value to get the portion of the 8 bits that described the next best candidate, move there. which in code and with a sx, sy as the starting coordinates for the path goes like:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
var path = []; path.push( sx, sy ); var count = direction == exports.LEFT || direction == exports.RIGHT ? w : h; var mask = exports[ "MASK_" + direction ]; var id = ( ( sy * w ) + sx ) * 4; while( count-- ) { //get current pixel direction value ( val = 0, 1 or 2 ) var val = ( data[ id + 1 ] & mask ) >> direction ; if( direction == exports.TOP ){ sx += ( val == 0 ? -1 : ( val == 1 ) ? 0 : 1 );//choose least energy path sy--;//go up } if( direction == exports.RIGHT ){ sx++;//go right sy += ( val == 0 ? -1 : ( val == 1 ) ? 0 : 1 );//choose least energy path } if( direction == exports.BOTTOM ){ sx += ( val == 0 ? -1 : ( val == 1 ) ? 0 : 1 );//choose least energy path sy++;//go down } if( direction == exports.LEFT ){ sx--;//go left sy += ( val == 0 ? -1 : ( val == 1 ) ? 0 : 1 );//choose least energy path } id = ( ( sy * w ) + sx ) * 4; path.push( sx, sy ); } |
depending on the direction, the sx or sy values are linearly incremented or decremented while the other component is incremented using the precomputed values. the mask prevents other bits to interfere in the retrieval of the next pixel’s id. for instance masking 10010010 with 192 will leave the first 10 on the left, masking it with 48 will leave the following 01, with 12 you get the next 00 and with 3, the last 10. so for this pixel the least energy path up would be it’s TR, to it’s right, RI, at the bottom BL and on it’s left, BL.
here a gif of the results:
less noisy pictures give better results
further filtering images ( contrast, sobel, threshold, etc. ) improves the path’s quality and is the (rough) basis for so called intelligent scissors aka livewire segmentation.
as mentioned above, quilting is a special, unsophisticated use case and I believe this approach should be enough.
here’s a live version on codepen: least energy path
enjoy :)
Interesting !
I need to read the beginning maybe 5 times before I understood what you tryed to do (the results are not obvious when you just look at the demo without read the beginning again and again ) , but it’s interesting ! – and when you know what happen, it looks great ! (but I would like to see more example to be totally sure it works as great as expected, because it’s not so obvious :) )
What is the final goal of that stuff ?
(Sorry I didn’t see the live version)
To be honest, I ‘m not sure to understand your results.
The results are interesting because something is working, and sometime it works even great, but sometimes the path should be simple and it’s not.
I may be wrong but I think the issue you got in your “path finder” come from the fact you don’t store the previous angle between the “previous-previous-point” and the “previous point” . From that angle, you should define the starting value of “i” in your loop concerning the neightboors , then you ll be sure to move all the time using the less iteration possible (because the motion becomes logical, and because the motion is logical you will dodge some issues in the final result ). You also could try to optimise the path you got and rework from that optimised path.
What is the final goal ? (bis)
I may try, it’s definitly interesting !